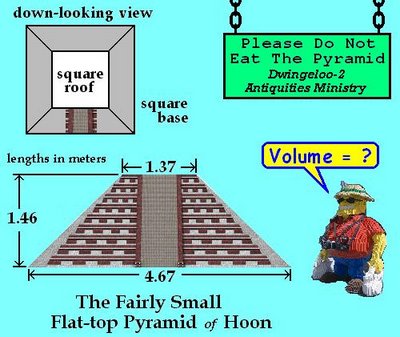
computation of volume of Fairly Small Flat-Top Pyramid of Hoon
Click all you want.
To be perfectly honest, Vleeptron is totally disgusted with the News from Earth this week, so we are not only fleeing to Vleeptron on the Zeta Beam, but we are also escaping to the only Realm of the Intellect that doesn't make us feel soiled and ashamed: Mathematics.
~ ~ ~
The Vodeeodo are a vanished, ancient people of the jungles of Planet Hoon, renowned for building their sacred architecture out of halvah. Subsequent people of Hoon have eaten nearly all the ancient buildings of the Vodeeodo, but the recently-discovered Fairly Small Flat-top Pyramid is the only building left.
The people of Hoon are notoriously crappy mathematicians. After discovering the Pyramid, they measured its dimensions carefully, but no one on Hoon has been able to compute the Volume of the halvah Pyramid. (The ancient Egyptians knew how to do this.)
5 slices of Pizza with double anchovies:
What is the Volume
(in cubic meters) of the
Fairly Small Flat-top Pyramid of Hoon?
(in cubic meters) of the
Fairly Small Flat-top Pyramid of Hoon?
If you don't care, or can't do it, maybe there's a child in your household who doesn't care either, but needs practice in geometry and algebra. Force the child to compute the Volume, and then share the Pizza with the child.


4 Comments:
Bob:
Head on over to my 'blog and look to see what I did this weekend.
vol = 1/3h(ab+cd+sqr[abcd])
a=4.67
b-4.67
c=1.37
d-1.37
h=1.46
.4867(21.8089+1.8769+sqr[40.9331]) = 14.6417 m^3
hey hey hey u win the 5 slices of pizza!
the ancient Egyptians -- pretty spiffy pyramid guys -- knew this formula. but somebody in our recent times proved that this formula can't be PROVEN except using the calculus (circa 1670 AD) because it requires the concept of Continuity.
But that was the way of the Egyptians -- if it worked, the heck with proving it. And I guess it worked. Them pyramids is still there. (Will Cuppy I think pointed out that it's not really all that astonishing that the Pyramids are still standing. What else could they do? They couldn't fall down if they tried.)
well, this one is one step harder than calculating the volume of a regular pyramid because it is truncated at the top.
The formula for the volume of a regular pyramid is 1/3 a*b*h where a and b are the sides of the base and h is the height. Truncating it means that somehow you have to figure the area of the bit that you have removed and subtracting it from the volume. Turns out that the bit that is removed is mathematically related to the square of the volume of the whole thing. Simple, really, and very elegant.
Post a Comment
<< Home