more about the Fairly Small Flat-Top Halvah Pyramid of Hoon

Yes, of course you should click.

Earthers think the Turks invented halvah, but actually halvah was invented by the vanished jungle people of Hoon, the Vodeeodo. I brought some back on the Zeta Beam, then travelled back in time in my Heathkit TM-212, and gave it to a Turkish guy in 1050 AD.

The Vodeeodo considered Halvah a Sacred Food, and only Royalty and the Priests were allowed to eat it. If they caught an Ordinary Guy eating halvah, they would immediately seize and disembowel him.

They made halvah into square sheets of such incredible thinness that when you put a piece on your tongue, Taste was the only sensation -- your tongue and teeth could detect no mass or bulk, there was no chewing required, it just melted into deliciousness on your tongue.

Eventually they began building their Sacred Pyramids by stacking gazillions of incredibly thin halvah sheets one on top of the other. As mentioned earlier, the Fairly Small Flat-Top Pyramid of Hoon is the only one left; travellers and tourists long ago ate all the other Pyramids.

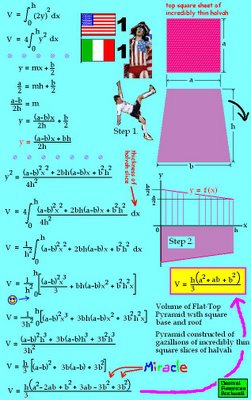
Given such a Pyramid built of incredibly thin square halvah sheets, how can we derive the Volume Formula which won Jim the pizza slices?

If the LENGTH of a side of each square sheet is s units,

then its AREA is s^2 units squared.

Each sheet is so incredibly thin that it's impossible to assign a number to its thickness, so we just call the thickness dx .

Make no mistake -- dx IS really a dimension, it's Not Nothing. But if we insisted on assigning it a number like 0.000000000000000002 units, it would be cumbersome and unwieldy -- and still too large a number to accurately express the incredible thinness of the halvah.

So the VOLUME of each sheet of halvah is

s^2 x dx

or

s^2 dx units cubed

Now if

h = the height of a Pyramid

b = the length of a side of its square base

a = the length of a side of its square roof

we want to derive the simple Volume Formula

V = (h/3)(a^2 + ab + b^2)

Step 1. Kick the Fairly Small Pyramid and knock it over on its side.

Step 2.Skewer the centers of the bottom and top halvah sheets with a long, incredibly thin knitting needle. If you want to call this knitting needle the x-Axis , that's okay with me and Rene Descartes.

Now we want to juggle the measured lengths a, b and h to find the equation

y = f(x)

for the straight line from the midpoint of the side of the base to the midpoint of the side of the roof.

With this equation, no matter which halvah sheet we choose, we'll know exactly what the length of a side of it is at that height of the Pyramid: 2y units

And that sheet's AREA will be (2y)^2 = 4y^2 units squared

and that sheet's VOLUME will be 4y^2 dx units cubed

If we could Sum the Volumes of All These halvah sheets, we'd know the VOLUME of the whole Pyramid.

That's what that screwy Integral Symbol is -- a Sum. That's why Leibniz made it look like a stretched out S.

We're going to Sum the Volumes of all halvah sheets
from the Pyramid's Base (x = 0) to its Roof (x = h) .

Get a Big Bottle of Extra Strength Aspirin. (Canadians may use Over-The-Counter Aspirin with Halvah.)

The y equation isn't too hard to figure out. Things start to get algebraically jiggy when we multiply it by itself to find y^2 . Now take the first 2 aspirin.

Down by the Smiley Face, we Evaluate The Definite Integral.

The Face Is Smiling because the Lower Limit x = 0 . Because each of the 3 terms contains a factor x , and 0 times anything = 0 , this effectively halves the Algebra Nightmare we have to endure. We only have to evaluate this nasty expression for the Upper Limit x = h .

Four lines below, A Wonderful Algebra Miracle Happens, and the whole verkakte mess collapses nicely into the simple Volume formula. Please do not eat the Pyramid.

P.S. If you don't kick the Pyramid over on its side, then you end up with

x = f(y)

which is perverted and Against The Law, and I don't know how to evaluate stuff like that.